What Is A Degenerate


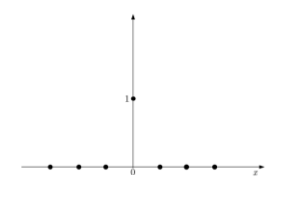
CDF for k0=0. The horizontal axis is x. | |||
| Parameters | |||
|---|---|---|---|
| Support | |||
| PMF | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | undefined | ||
| Ex. kurtosis | undefined | ||
| Entropy | |||
| MGF | |||
| CF | |||
From Wikipedia, the free encyclopedia Degenerate matter is a highly dense state of fermionic matter in which the Pauli exclusion principle exerts significant pressure in addition to, or in lieu of thermal pressure. The description applies to matter composed of electrons, protons, neutrons or other fermions.
- Degenerate: 1 n a person whose behavior deviates from what is acceptable especially in sexual behavior Synonyms: deviant, deviate, pervert Types: show 9 types. Fetishist one who engages in fetishism (especially of a sexual nature) masochist someone who obtains pleasure from receiving punishment nympho, nymphomaniac a woman.
- Degenerate matter is matter whose properties are determined by quantum mechanics. This matter can behave very differently to the matter that we are familiar with; you can call degenerate matter the counterpart of matter that respects the ideal gas law. Matter becomes degenerate under the enormous pressures of very dense stellar remnants.
In mathematics, a degenerate distribution is a probability distribution in a space (discrete or continuous) with support only on a space of lower dimension. If the degenerate distribution is univariate (involving only a single random variable) it is a deterministic distribution and takes only a single value. Examples include a two-headed coin and rolling a die whose sides all show the same number. This distribution satisfies the definition of 'random variable' even though it does not appear random in the everyday sense of the word; hence it is considered degenerate.
In the case of a real-valued random variable, the degenerate distribution is localized at a point k0 on the real line. The probability mass function equals 1 at this point and 0 elsewhere.
The degenerate univariate distribution can be viewed as the limiting case of a continuous distribution whose variance goes to 0 causing the probability density function to be a delta function at k0, with infinite height there but area equal to 1.
What Is A Degenerate Triangle
The cumulative distribution function of the univariate degenerate distribution is:
Constant random variable[edit]
In probability theory, a constant random variable is a discrete random variable that takes a constant value, regardless of any event that occurs. This is technically different from an almost surely constant random variable, which may take other values, but only on events with probability zero. Constant and almost surely constant random variables, which have a degenerate distribution, provide a way to deal with constant values in a probabilistic framework.
Let X: Ω → R be a random variable defined on a probability space (Ω, P). Then X is an almost surely constant random variable if there exists such that
and is furthermore a constant random variable if
Note that a constant random variable is almost surely constant, but not necessarily vice versa, since if X is almost surely constant then there may exist γ ∈ Ω such that X(γ) ≠ k0 (but then necessarily Pr({γ}) = 0, in fact Pr(X ≠ k0) = 0).
For practical purposes, the distinction between X being constant or almost surely constant is unimportant, since the cumulative distribution functionF(x) of X does not depend on whether X is constant or 'merely' almost surely constant. In either case,
The function F(x) is a step function; in particular it is a translation of the Heaviside step function.
Higher dimensions[edit]
Degeneracy of a multivariate distribution in n random variables arises when the support lies in a space of dimension less than n. This occurs when at least one of the variables is a deterministic function of the others. For example, in the 2-variable case suppose that Y = aX + b for scalar random variables X and Y and scalar constants a ≠ 0 and b; here knowing the value of one of X or Y gives exact knowledge of the value of the other. All the possible points (x, y) fall on the one-dimensional line y = ax + b.
In general when one or more of n random variables are exactly linearly determined by the others, if the covariance matrix exists its determinant is 0, so it is positive semi-definite but not positive definite, and the joint probability distribution is degenerate.
Degeneracy can also occur even with non-zero covariance. For example, when scalar X is symmetrically distributed about 0 and Y is exactly given by Y = X2, all possible points (x, y) fall on the parabola y = x2, which is a one-dimensional subset of the two-dimensional space.
Degenerate matter is matter whose properties are determined by quantum mechanics. This matter can behave very differently to the matter that we are familiar with; you can call degenerate matter the counterpart of matter that respects the ideal gas law. Matter becomes degenerate under the enormous pressures of very dense stellar remnants.
If the core of a star is compressed, the atoms and the electrons in the core get closer and closer to each other. Normally such a compression happens if the temperature in the core decreases and as a consequence the thermal pressure that counteracts the force of gravity decreases too. But the electrons cannot get closer to each other than the laws of quantum mechanics allow. According to these laws it is not possible that more than two electrons in the same atom can have the same quantum state. This means that if matter is compressed to a certain degree, the Pauli Exclusion Principle generates a counter pressure called degeneracy pressure which prevents further contraction of the matter. Due to this degeneracy pressure the matter can support a much higher pressure than it would be able to support without degeneracy. One important consequence is that the pressure of degenerate matter does not depend on temperature any more as is the case for normal matter when increasing its temperature causes a gas to also increase its pressure (see ideal gas law). Amongst others this fact plays a crucial role with supernova Type Ia. Now, by further increasing the pressure on degenerate matter there is still no further compression due to the Pauli Exclusion Principle, but instead the speed with which the electrons move increases. This way the pressure on degenerate matter can still be increased without collapse of the matter. Anyhow, if pressure is increased to a certain point (the Chandrasekhar limit) the electrons approach the speed of light. There is nothing in this universe that can reach or exceed the speed of light. At this point degeneracy pressure is no longer able to support the pressure of the matter and the matter suddenly collapses. In astronomy this happens with core collapse supernovae (Type II, Type Ib and Type Ic supernova).
The next 'stop' of the matter is a neutron star. Most of the electrons and protons of the progenitor star have been literally pressed into each other by the enormous pressure, forming neutrons. You can imagine the neutron star as a gigantic nucleus consisting of almost nothing but neutrons. It is extremely compact. To understand this better, imagine the size of a normal atom to be as big as a football stadium. In such an atom the nucleus would be the size of a grain of rice at its centre. All the other space would be empty with just the even smaller electrons flying around in it. A neutron star is so compact because the former atom (or football stadium) is now squeezed into the size of just the nucleus (or rice grain) itself. In effect, the neutron star still consists of single atomic nuclei, but packed together almost seamlessly.
Now, the Pauli Exclusion Principle is not only valid for electrons but for any particles called fermions (which are all half integer spin-particles like protons, neutrons, muons and others). So, instead of electron degeneracy the neutron star is held up against collapse from neutron degeneracy with the main difference that the neutron degeneracy pressure is much higher. The same Pauli Exclusion Principle applies; a neutron must occupy its own quantum state (or space) and cannot be compressed further. If we apply even higher pressure again by adding more matter to the neutron star, this leads to higher speeds of the vibrating neutrons. If the mass of a neutron star reaches 3 solar masses the speed of the neutrons again reaches the speed of light and the neutron star cannot support its own weight anymore. This limit is called the Tolman-Oppenheimer-Volkhof limit; it's analogous to the Chandrasekhar limit of electron degenerate matter. The neutron star collapses to a theoretical object called a quark star. These quark stars have not been discovered and are only a hypothesis at this time.

What Is A Degenerate Triangle
Indeed they lie completely inside the Schwarzschild radius of the black hole that will be created when a neutron star collapses. The maximum mass of such a black hole that has formed from an individual star is about 10 solar masses, the rest of the matter of the former star (individual stars can have masses of more than 100 solar masses) will be lost during the lifetime and the supernova event of the star.What Is A Degenerate Male
You can read more about the formation of neutron stars and black holes in our supernova article; more information about a neutron star can be found in the corresponding neutron star article on Sun.org.